Come calcolare deviazione standard di una media?

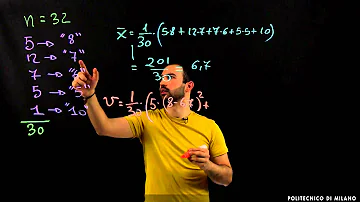
Come calcolare deviazione standard di una media?

In una distribuzione di frequenze la deviazione standard si calcola moltiplicando il quadrato della differenza ( xi - μ )2 per la frequenza Φi della modalità. Nota. Nel caso in cui si tratti di classi con intervalli di valori, si prende come riferimento il valore centrale della classe.

Cosa è la deviazione standard?

La deviazione standard è l'indice statistico che misura la dispersione delle singole osservazioni di un fenomeno intorno ad un valore atteso o alla sua stima.

Quando si usa la deviazione standard?

E' la dispersione delle singole osservazioni intorno alla media aritmetica ed è usata per valutare lo scostamento dal cosidetto "equilibrio". In statistica si chiama anche "radice quadrata della varianza" o "Scarto quadratico medio".

Quando la deviazione standard è alta?

Se la deviazione è molto alta, vuol dire che il titolo o il portafoglio considerato può avere una variabilità notevole dei risultati rispetto alla sua media.

Cosa significa 3 sigma?

Nelle scienze empiriche la cosiddetta regola empirica dei tre sigma esprime un'euristica convenzionale secondo cui quasi tutti i valori sono considerati entro tre deviazioni standard della media, e quindi è empiricamente utile trattare la probabilità del 99,7% come quasi certezza.

Come si calcola la media e la deviazione standard su Excel?

Excel ha la capacità di gestire i calcoli della deviazione standard sia per l'intera popolazione che per un campione di essa. Basta fare clic in una cella e iniziare a digitare =DEV.ST. Vedrete un menu a discesa con alcune funzioni di deviazione standard.

Come si calcola la deviazione standard del campione?

Nella formula della deviazione standard campionaria la somma delle differenze al quadrato viene divisa per N-1 anziché N. In questo modo, la deviazione standard campionaria calcolata in un campione tende a eguagliare la deviazione standard calcolata sull'intera popolazione.

Cosa si intende per media e deviazione standard?

La media rappresenta la media aritmetica delle misure del campione a cui siamo interessati. La deviazione standard, o scarto quadratico medio, è un indice di dispersione delle misure sperimentali. È uno dei modi per rappresentare la dispersione dei dati attorno al valore atteso.

Quando usare la varianza e quando la deviazione standard?

La varianza è un valore numerico che descrive la variabilità delle osservazioni dalla sua media aritmetica. La deviazione standard è una misura della dispersione di osservazioni all'interno di un set di dati. ... Al contrario, la deviazione standard misura la quantità di osservazioni di un set di dati diversa dalla media.

Come si interpreta la deviazione standard?

• La deviazione standard è la radice quadrata della varianza. Come si interpreta la deviazione standard? La deviazione standard è pari a 0 solo quando non c’è dispersione. Questa situazione si verifica solo quando tutte le unità statistiche hanno lo stesso valore. In tutti gli altri casi, lo scarto quadratico medio è sempre maggiore di 0.

Quando la deviazione standard è pari a 0?

• La deviazione standard è pari a 0 solo quando non c’è dispersione. Questa situazione si verifica solo quando tutte le unità statistiche hanno lo stesso valore. In tutti gli altri casi, lo scarto quadratico medio è sempre maggiore di 0. Quanto più i valori sono lontani dalla media, tanto più la deviazione standard sarà grande.

Qual è la deviazione standard di una variabile?

• La deviazione standard di una variabile è un indice riassuntivo delle differenze dei valori di ogni osservazione rispetto alla media della variabile. Ogni osservazione ha infatti uno scostamento (detto anche scarto o deviazione) dalla media. Questo scostamento è pari a 0 se l’osservazione ha esattamente lo stesso valore della media.